The Importance of Interceptions (or lack thereof)

I have spent quite a bit of time lately talking about interceptions.  In case you have any doubt that an interception can make a difference you got that answer on Super Bowl Sunday.  In probably one of the greatest plays in Super Bowl history (until the catch by Santonio Holmes with 35 seconds left that gave the Steelers a come-from behind victory), with Arizona on the Pittsburgh 1 yard line, first and goal, and 18 seconds left in the first half, the Steelers' James Harrison picked off Arizona's Kurt Warner and returned it all the way for a touchdown as time expired.  This was, in effect, a 13-point play, as Arizona's expected points at the Pittsburgh 1 was about 6 points.  Brian Burke, who I've highlighted before, has an excellent post on the subject on his site at advancednflstats.com.   

Take a look at the graph below.  The blue line (on the left scale) shows the league average QB passer rating (for those QBs who thew enough passes during the season to qualify) by year since 1940.  As you know, the NFL's QB passer rating formula has four components - completion percentage, yards per attempt, touchdown percentage, and interception percentage (see my previous posts on the subject here and here).  When it was designed in 1973, the formula used the 1972 season as a "base", and hence created adjustments to each component, such that the average would be a score of 1.00 for each component, resulting in a passer rating for 66.7 for a quarterback who had average statistics in each of the four categories.  The actual calculations for each of the four components in 1972 yielded the following four figures - 1.085, 0.954, 0.897, and 1.043, respectively, which in turn yielded the average quarterback passer rating of 66.3 (the figure for the qualified leaders turns out only slightly higher - 67.9).  Back then, each of the four components were essentially balanced.

Today, it's a different story.  If the system was balanced, then we would expect the interceptions component to make up about 25% of the quarterback passer rating score.  Looking at the graph again, and this time looking at the red line (on the right scale) shows how much the interceptions component influences the league's quarterback rating system.  It hasn't been below 30% since 1983, and the last time it was "around" 25% was actually 1971.  The point is that the NFL passer rating system is not what it used to be, and interceptions are the leading weight in today's NFL passer rating system.

Let's take a look at another example.  Tom Brady's record-breaking 2007 season.  That year, Brady completed 398 of 578 passes, for 4,806 yards, and threw for 50 touchdowns while only throwing 8 interceptions.  His passer rating that year - 117.2, is second only to Peyton Manning's all-time best 121.1 in 2004.  Most people will remember the 50 touchdowns that Brady threw.  Impressive as it was, it wasn't that impressive (I'll have a post later on this subject).  Most people will not remember that he only threw 8 interceptions in 578 attempts.  That ranks as 14th best all-time in terms of single-season interception percentage (see Exhibit 2), and, it accounted for 29% of his quarterback passer rating that year (his touchdowns accounted for 25%).

There are 7 exhibits on interceptions attached to this post.   Note that for all exhibits, I only considered those passers in any given year that threw enough passes to qualify - in other words, if a quarterback threw 20 passes during a season, that would not be enough to qualify him.  On the nfl.com site, the minimum qualification standard is 14 passes per game (so, for the 2008 season, the standard would be 14 * 16 = 224 passes).  The NFL uses this standard EVERY year.  

I think this universal standard is inappropriate.  Using this method for example, only three passers qualified in 1940.  The 14 passes comes from the fact that during the 50's, 60's and 70's, the average number of passes attempted by a team during a game was about 28.  Of course, we all know that this has changed over time.  The average number of passes attempted in a game by a team was 32.3 in 2008.  It has been below 30.0 once since 1979.  

The standards that I use varies by year, and reflects the average # of passes attempted during these years.  Here are the standards:

1940-1946 - 6.5

1947-1960 - 11.0

1961-1969 - 14.0

1970-1977 - 12.0

1978-1994 - 15.0

1995-2008 - 16.0

Using these standards, I get 1,451 quarterbacks in my database, with a low of 9 quarterbacks qualifying in each of 1941 and 1943, and a high of 32 quarterbacks qualifying in each of 1999 and 2005.  For 2008, I had 30 quarterbacks in my qualified database, whereas the NFL.com has 32.  So, not a big difference in recent years.  I just think that applying a universal standard across all these years is silly, especially when the game has changed so much.

In any case, now that we got the some of the technical stuff out of the way, here are the 7 exhibits:

Exhibit 1 - Chronological list of NFL leader (lowest) in interception percentage

Exhibit 2 - Best seasons in terms of interception percentage

Exhibit 3 - Best seasons in terms of standard deviations from the mean

Exhibit 4 - Worst seasons in terms of standard deviations from the mean

Exhibit 5 - Best (lowest) career interception rate (minimum of 1,000 passes attempted)

Exhibit 6 - Best career interception rate relative to league average

Exhibit 7 - Worst (highest) career interception rate relative to league average

Exhibit 1 - Chronological list:

Nothing spectacular here, it's simply each year's best.  I observe a few things: 

Clearly, the average interception rate has been decreasing every decade.  

The best quarterbacks in a given year seem to be around 1.8 standard deviations better than the average.

Slinging Sammy Baugh led the league 4 out of 6 years during the period from 1942 to 1947 - the only quarterback to have led the league on 4 separate occasions.  

6 quarterbacks - Bart Starr, Bobby Thomason, Charlie Conerly, Ken Anderson, Ken O'Brien, and Roger Staubach have led the league on 3 different occasions.

5 quarterbacks led the league in consecutive seasons - Sammy Baugh, Bobby Thomason, Milt Plum, Ken Anderson and Ken O'Brien.

Only 2 quarterbacks in history, Steve DeBerg in 1990 (0.90%), and David Garrard in 2007 (0.92%) completed a season where less than 1 percentage of their attempted passes were intercepted (this is not entirely evident by looking at Exhibit 1, but can be confirmed by Exhibit 2).  What's most unusual about DeBerg's performance that year was the fact that of the four interceptions he threw during the season, three of them were in one game!  In other words, he threw 1 INT the rest of the season.  Let's take a look at Exhibit 2.

Exhibit 2 - Best seasons in terms of interception percentage:

So indeed, only 2 quarterbacks have had seasons with fewer than 1% interceptions.  The list below is the kind of list that would show up in a record book.  

You'll see, for example, that Jason Campbell's 2008 season ranks in the top 5 all-time, and 2 other quarterbacks in 2008, Chad Pennington and Jeff Garcia, also had noteworthy seasons, with both finishing in the Top 30 all-time.  

If you look carefully, you'll notice that the list is dominated by quarterbacks in the past 2 decades.  Of the Top 50, 45 have occurred since 1990.  21 last decade and 24 this decade.  The 5 seasons in the top 50 not to have occurred in the last 19 years are Steve Bartkowski's 1983 season (#3), Bart Starr's 1966 and 1964 seasons, respectively (#7 and #18), and Ken O'Brien's 1985 and 1988 season's respectively (#36 and #38).  

So, what are we saying?  Are we saying that quarterbacks prior to 1990 were not very good?  No, not at all.  The league has changed.  From Exhibit 1, you can see that the average interception rate has been decreasing every decade.  So, we simply can't just compare a quarterback from one decade to another.  That's where Exhibit 3 comes in.  Let's take a look at that.

Exhibit 3 - Best seasons - Interceptions percentage, ranked by how different the particular season was compared to the mean, using the standard deviation as the measuring stick:

Wow, what a difference.  You can quickly see that this is a much better representation of the past 7 decades.

1940's - 3

1950's - 2

1960's - 10

1970's - 9

1980's - 7

1990's - 6

2000's - 13

Look at Bart Starr!  Ranked twice in the Top 5, and 3 times in the Top 25.  

And, this measure doesn't discount Steve DeBerg's and David Garrard's great seasons - they're both still in the Top 5.  But it does give one a bit more perspective.  In other words, this suggests that Bart Starr's 1962 season (which ranks #430 in absolute terms), when compared to everyone else's performance during that season, was better than David Garrard's performance, when compared to how all the other quarterbacks did in 2007.

Now for a little math.  Why are we using standard deviation as a measure of separation?  And why does using it make comparing quarterbacks across years more meaningful?  

A non-technical definition of the standard deviation is that it is a measure of the dispersion of a set of data around the average.  By dispersion we mean spread.  Knowing the average of the data, and knowing how spread the data is, we can try to determine how likely a given observed value is.  We can use this data to compare different data sets, and relate them to one another.   So for example, in a data set where the average is 5, and the standard deviation is 2, an observation of 8, would mean 1.5 standard deviations ((8-5)/2 = 1.5) above the the mean.  In a data set where the average was 7, and the standard deviation was 4, a value of 13 would also be 1.5 standard deviations from the mean.   You can now see why the use of a standard deviation could be useful in comparing different sets of data.  

As you can see from Exhibit 1, the league average interception rate has been changing over time.  In addition, while I have not shown it explicitly, the standard deviation around the mean has also been changing.  As a matter of fact, in the early 1940's, the standard deviations were quite high because there were fewer players involved, the number of attempted passes were fewer, and arguably the talent pool was not as great (i.e. passing was a fairly new concept).  

By relating a given observation of an interception rate in 1943 to the mean interception rate that year, and the standard deviation of interception rate that year, one can then compare that particular observation to an observation of an interception rate in 2003, by its relationship to the mean and standard deviation of interception rates in 2003.  If one assumes, in particular,  that in any given year, that all observations about the mean are distributed normally (i.e. a "bell-shaped" curve), then the comparisons become that much more meaningful.  For example we know that in a standard bell-curve, that approximately 68% of the observations will fall into a band +/- 1 standard deviation from the mean, and approximately 95% of observations will fall into a band +/- 2 standard deviations from the mean.  Also, if, after relating the observations in each year to each year's mean and standard deviation, one aggregates the data across all years (since the data has been "normalized" to the same scale - a number in relation to a mean and standard deviation; in the example earlier, the observation of 8 in the first data set has the same value on a normalized basis as the observation of 13 in the second data set - 1.5), then the aggregated data should look like a standard normal curve, with a mean of 0, and a standard deviation of 1.  

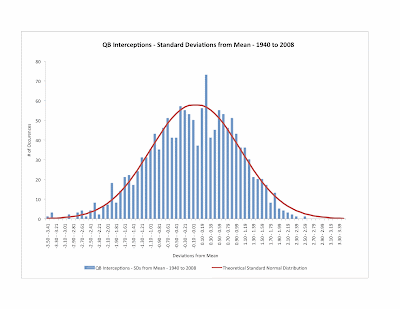
Well, I went through the trouble of doing that, and guess what - that is exactly what the looks like.  All 1,451 qualified passers over the 69 years from 1940 to 2008 were analyzed in this manner, and the result is in the graphical illustration below.  The average for the entire data set is -0.06 (close to 0), and the standard deviation is 1.00!  Also, it turns out that 69% of the observations are within +/- 1 standard deviation, and 96% are within +/- 2 standard deviations.  Quite a remarkable achievement!  I've graphed a standard normal distribution as well, so that you can see for yourself how close the actual data is to the theoretical curve.

Exhibit 4 - Same as Exhibit 3, except ranks the worst seasons:

Terry Bradshaw's 1970 rookie season ranks as the all-time worst.  And Vinny Testaverde's 1998 campaign is not that far behind.  Although Testaverde's rookie season was 1987, he didn't "get exposed" until 1988.  Most recently, Gus Frerotte's 2008 campaign was an absolute disaster.  There's some names on the list that I would not have expected to see (let's face it, these are the 50 worst performances over the past 69 years - 1,451 quarterback seasons) - names like Favre and Aikman, along with the aforementioned Bradshaw.  What was even more surprising to me was that they each showed up not once, but twice!

So now you've seen the best and the worst seasons.  How about careers?  Let's take a look at Exhibit 5.

Exhibit 5 - Lowest career interception rate - absolute figures - with a minimum of 1,000 passes attempted:

For reasons I discussed above, I don't like this list that much, as it is biased towards the more recent years.  But, since people like looking at these types of lists, I have included it.  Exhibits 6 (best) and 7 (worst) reorder the data after a player's career has been compared to the average during their career.

Exhibits 6 (best/lowest) and 7 (worst/highest) - career interception rate relative to league average during the same time:

First question is: why, after the long dissertation about standard deviations, am I not using that as the measuring stick?  Simple answer - it's difficult!  It was a relatively simply exercise to calculate standard deviations for each year.  And it's not that difficult to do it for a given set of consecutive years.  Where it becomes increasingly difficult is to do it for every combination of multiple years, over a 69-year period.  At some point before the 2009 NFL season, I'll have it done.  That will be a better reflection of who had good or bad careers, but, in the meantime, this will have to suffice.  It's the next best thing.  It is most certainly better than the absolute comparison shown in Exhibit 5.

Ok, on to a few observations.

Exhibit 6 is a who's who of quarterbacks in football history.  Taking out the 13 players who are either currently playing, or who have retired in the past five years (i.e. not Hall of Fame eligible), 14 of the remaining 37 are in the Hall of Fame.  Let's look at it another way.  There are 27 quarterbacks who are in the Hall of Fame, who played football post 1940.  And two of them, Arnie Herber, and Clarence (Ace) Parker, played much of their careers before 1940.  Of the remaining 25, 14 show up in Exhibit 6.  

Who are the 14?

Joe Montana (#3)

Roger Staubach (#9)

Steve Young (#14)

Sammy Baugh (#19)

Fran Tarkenton (#20)

Bart Starr (#22)

Sonny Jurgensen (#23)

Otto Graham (#32)

Dan Marino (#33)

Sid Luckman (#37)

John Elway (#39)

Len Dawson (#42)

Johnny Unitas (#46)

Norm Van Brocklin (#50)

And 2 more, Y.A. Tittle (#53), and Troy Aikman (#55) just missed being in the Top 50.  Not a bad list.

What about Exhibit 7?  3 Hall of Famers, Joe Namath, George Blanda, and Terry Bradshaw are in the worst 50 all-time, in terms of their career interception percentage as it relates to the league average during the time that they played.